Unit 8 Test

  1. A visitor to a lighthouse wishes to determine the height of the tower. She ties a spool of thread to a small rock to make a simple pendulum, which she hangs down the center of a spiral staircase of the tower. The period of oscillation is 9.40 s. What is the height of the tower?
  2. Transverse waves travel at 20.0 m/s on a string that is under a tension of 6.00 N. What tension is required for a wave speed of 30.0 m/s in the same string?

    Solutions for1&2

  3. A 5.0 kg mass on the end of a spring oscillates on a frictionless, horizontal surface with the equation for its position given by x(t) = .25 m sin[(3.2 rad/s)t + .13]. (a) Find the maximum velocity and acceleration of the mass. (b) What are the velocity and acceleration at time t=0 s? (c) What is the spring constant for this system?
  4. A 2.3 kg mass is placed between two walls on a frictionless, horizontal surface. The mass is connected to each wall with a spring. The spring on the left has a spring constant of 55 N/m; the one on the right, 85 N/m. Both springs are .2 m in length and are unstretched when attached to the mass. The mass is moved .05 m to the left. What is the equation for the position of the mass as a function of time?

    Solutions:3&4

  5. One apparatus used to measure the speed distribution of gas molecules consists of two slotted rotating disks spearated by a distance s, with the slots displaced by the angle theta = q. Suppose the speed of light is measured by sending a light beam toward the right disk of this apparatus. (a) Show that a light beam will be seen in the detector (that is, will make it through both slots) only if its speed is given by c = sw/q, where w is the angular speed of the disks and q is measured in radians. (b) What is the measured speed of light if the distance between the two slotted rotating disks is 2.5 m, the slot in the second disk is displaced 1/60 of one degree from the slot in the first disk, and the disks are rotating at 5555 rev/s?

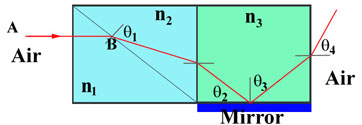
  6. A light ray follows the path shown in the above figure. Given that n1 = 1.7, n2 = 1.5, n3 = 1.3, and q(theta) = 60o, determine the anglesq1, q2, q3, and q4. Assume that the index of refraction for air is 1.0 and path AB is parallel to the base of the figure.

  7. A material with index of refraction n = 2.0 is in the shape of a quarter circle of radius R = 10 cm and is surrounded by a vacuum. A light ray, parallel to the base of the material, is incident from the left at a distance of L=5.0 cm above the base and emerges out of the material at an angle phi. Determine the value of phi.

    8. Solutions:5,6 & 7

  8. The real image height of a concave mirror is observed to be four times greater than the object height when the object is 30.0 cm in front of a mirror. What is the radius of curvature of the mirror?
  9. A goldfish is swimming in water inside a spherical plastic bowl of index of refraction 1.33. If the goldfish is 10.0 cm from the wall of the 15.0-cm-radius bowl, where does the goldfish appear to an observer outside the bowl?
  10. A converging lens has a focal length of 20.0 cm. Locate the images for object distances of (a) 40.0 cm, (b) 20.0 cm, and (c) 10.0 cm. For each case, state whether the image is real or virtual and erect or inverted, and find the magnification.

Solutions:8,9 & 10